Pythonで主成分分析による次元削減を行い、プロットで可視化

主成分分析（PCA）は、多変量データの次元削減手法の一つであり、データの特徴を把握するために広く用いられています。Pythonには、NumPyやscikit-learnなどのライブラリがあり、これらを利用することで簡単に主成分分析を実行することができます。

主成分分析（PCA）とは何か

主成分分析は、多変量データの次元削減手法の一つであり、データの特徴を把握するために広く用いられています。主成分分析では、元のデータにおける分散が最大になるような新たな軸を見つけ出し、データをその軸上に射影することで、元のデータの特徴をより少ない次元で表現することができます。

Pythonと主成分分析の関係性

Pythonには、NumPyやscikit-learnなどのライブラリがあり、これらを利用することで簡単に主成分分析を実行することができます。また、matplotlibなどのライブラリを用いることで、主成分分析の結果を可視化することができます。

Pythonによる主成分分析の基本的な手順

Pythonによる主成分分析の基本的な手順は以下の通りです。

  1. データの読み込み
  2. データの標準化
  3. 共分散行列の計算
  4. 固有値・固有ベクトルの計算
  5. 主成分の選択と次元削減

次元削減の意義と主成分分析による実施方法

次元削減は、多変量データを解析する際に、データの次元数を削減することで、データの特徴を簡潔に表現することができます。主成分分析は、次元削減の手法の一つであり、元のデータにおける分散が最大になるような新たな軸を見つけ出し、データをその軸上に射影することで、元のデータの特徴をより少ない次元で表現することができます。

Pythonを用いた主成分分析の実施方法は以下の通りです。

import numpy as np
from sklearn.decomposition import PCA
# データの読み込み
data = np.loadtxt('data.csv', delimiter=',')
# データの標準化
data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
# 主成分分析の実行
pca = PCA(n_components=2)
pca.fit(data)
result = pca.transform(data)
# 結果の表示
print(result)

Pythonを用いた主成分分析の結果のプロットとその読み解き方

Pythonを用いた主成分分析の結果のプロットとその読み解き方は以下の通りです。

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# データの読み込み
data = np.loadtxt('data.csv', delimiter=',')
# データの標準化
data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
# 主成分分析の実行
pca = PCA(n_components=2)
pca.fit(data)
result = pca.transform(data)
# 結果のプロット
plt.scatter(result[:, 0], result[:, 1])
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

プロットされたグラフは、主成分1と主成分2による座標系で表されています。各データ点は、元のデータを主成分1と主成分2の軸上に射影した結果です。主成分1と主成分2によって、元のデータの特徴をより少ない次元で表現することができます。

実際のデータを用いた主成分分析の実行例

以下は、実際のデータを用いた主成分分析の実行例です。

import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# データの読み込み
data = np.loadtxt('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv', delimiter=',', skiprows=1, usecols=[0, 1, 2, 3])
# データの標準化
data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
# 主成分分析の実行
pca = PCA(n_components=2)
pca.fit(data)
result = pca.transform(data)
# 結果のプロット
plt.scatter(result[:, 0], result[:, 1])
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

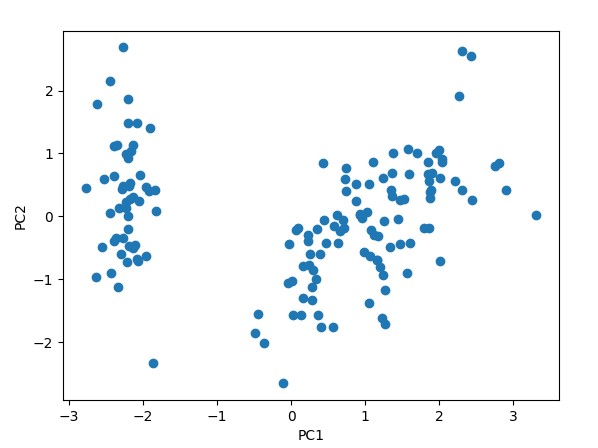
上記の例では、Irisデータセットを用いて主成分分析を実行しています。主成分1と主成分2によって、アヤメの種類を分類することができます。

まとめ

Pythonを用いた主成分分析による次元削減を行い、プロットで可視化することができます。主成分分析は、多変量データの特徴を把握するための有用な手法の一つであり、Pythonを用いることで簡単に実行することができます。