Pandasでpolyfitを使った多項式回帰分析：詳細ガイド

はじめに

多項式回帰分析は、データの傾向を表す非線形の曲線を近似することができます。この分析を実行するために、PythonのPandasライブラリとNumPyのpolyfit関数を使うことができます。

この記事では、多項式回帰分析の基本概念、Pandasとpolyfitの連携方法、polyfitの主要なパラメータとオプション、実例、評価指標などについて詳しく説明します。

多項式回帰分析の基本概念：線形回帰との違いと利用シーン

線形回帰は、独立変数と従属変数の間に線形の関係がある場合に使われます。一方、多項式回帰分析は、独立変数と従属変数の間に非線形の関係がある場合に使われます。

例えば、以下のような散布図がある場合、線形回帰では傾向を正確に表現できない可能性があります。

しかし、多項式回帰分析を使用することで、傾向を表す曲線を正確に近似することができます。

Pandasとpolyfitの連携：データフレームから多項式回帰分析を実行する方法

まず、必要なライブラリをインポートします。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

次に、データを読み込みます。以下の例では、CSVファイルからデータを読み込んでいます。

df = pd.read_csv('data.csv')

次に、xとyの値を抽出します。

x = df['x'].values
y = df['y'].values

そして、NumPyのpolyfit関数を使用して、多項式回帰分析を実行します。以下の例では、2次の多項式回帰分析を実行しています。

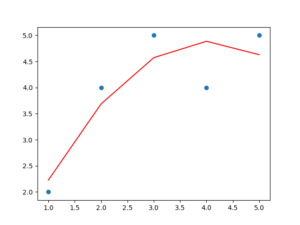
# 2次の多項式回帰分析を行う
coefficients = np.polyfit(x, y, 2)
p = np.poly1d(coefficients)

# グラフを描画
plt.scatter(x, y)
plt.plot(x, p(x), color='red')
plt.show()

これにより、次のような結果が得られます。

多項式回帰分析のプロット

polyfitの主要なパラメータとオプション：degree, rcond, full, w, cov

polyfit関数にはいくつかのパラメータがあります。主なものを以下に紹介します。

  • degree: 多項式の次数を指定します。例えば、2を指定すると2次の多項式回帰分析が実行されます。
  • rcond: ランク付けの閾値を指定します。デフォルト値は-1で、最適な値が自動的に選択されます。
  • full: フル出力を有効にするかどうかを指定します。デフォルト値はFalseで、必要なデータだけが返されます。
  • w: 重みを指定するためのパラメータです。デフォルト値はNoneで、すべての点が等しい重みを持つと見なされます。
  • cov: 返される共分散行列の種類を指定します。デフォルト値はFalseで、共分散行列は返されません。

多項式回帰分析の実例：具体的なデータフレームでの実践

以下は、実際のデータフレームを使用した多項式回帰分析の例です。

data = {'x': [1, 2, 3, 4, 5], 'y': [1, 3, 5, 7, 9]}
df = pd.DataFrame(data)
# extract x and y values
x = df['x'].values
y = df['y'].values
# fit a 2nd degree polynomial
coefficients = np.polyfit(x, y, 2)
# create a polynomial function based on the coefficients
p = np.poly1d(coefficients)
# create a range of x values for plotting the curve
x_range = np.linspace(x.min(), x.max(), 100)
# plot the data and the curve
plt.scatter(x, y)
plt.plot(x_range, p(x_range), color='red')
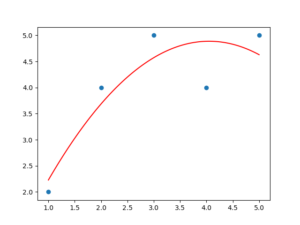
plt.show()

これにより、以下のような結果が得られます。

評価指標と適用範囲：多項式回帰分析の結果を評価する方法

多項式回帰分析の結果を評価するために、以下の評価指標を使用することができます。

  • 決定係数（R2）: モデルがデータにどの程度適合しているかを示す指標です。R2は0から1の範囲であり、1に近いほどモデルがデータに適合していることを示します。
  • 平均二乗誤差（MSE）: モデルの予測が実際の値からどの程度離れているかを示す指標です。MSEは小さいほどモデルの予測が正確であることを示します。

適用範囲については、多項式回帰分析はあくまでもデータの傾向を表す曲線を近似するものであり、予測を行うための正確なモデルではありません。そのため、予測を行う際には注意が必要です。

まとめ

PandasとNumPyを使って、多項式回帰分析を実行する方法について説明しました。また、polyfit関数の主要なパラメータや、多項式回帰分析の評価指標、適用範囲についても説明しました。多項式回帰分析は、非線形のデータを分析する際に有用な手法であり、PythonのPandasとNumPyを使うことで簡単に実行することができます。